

The GeMA (Geo Modelling Analysis) application is a powerful multiphysics, multiscale simulator capable of handling complex problems that may involve multiple physics processes, interacting in different spatial and time scales.
The application is built upon the GeMA framework, a library intended to support the
development of new multiphysics simulators and their integration with existing
ones.
GeMA uses software engineering techniques to allow engineers to focus on the programming
of
the physical simulation and let the framework take care of data management and other
necessary support functions to develop efficient, professional programs. GeMA
architecture
supports
multiple simulation and coupling paradigms, with particular emphasis given to the finite
element method (FEM). A central point is that the framework does not dictate how each
physics is simulated or how multiple physics are coupled. Those decisions can be made by
engineers according to the scenario at hand.
The GeMA framework supports the coupling of different physics, each with possibly different spatial domain discretizations (meshes). It has functions to support an efficient transfer of state variable values from one discretization to another using several available interpolation options. The framework also implements some important concepts of extensibility, through the combined use of plugins and abstract interfaces, configurable orchestration and fast prototyping through the usage of the Lua language.
Combined with Jade, our analysis and design environment for effortlessly creating
simulation
models based on pre-defined templates, GeMA can easily solve a large number of real-life
geomechanical problems.
The GeMA framework's first version was released in 2016 and is in continuous use and
evolution since then, having been used in several industry projects at the Tecgraf /
Puc-Rio
institute, as well as in dozens of published academic works. Its evolution was partially
supported by Shell projects through the ANP (Brazilian National Oil, Natural Gas and
Biofuels Agency) R&D levy regulation.
GeMA includes full THMC capabilities to handle geomechanical analysis, single-phase fluid flow, thermal analysis and reactive transport problems...
GeMA includes full THMC capabilities to handle geomechanical analysis, single-phase fluid flow, thermal analysis and reactive transport problems, among others, all of them based on the Finite Elements Method. The required physics can be strong or weakly coupled. It also supports multiple constitutive models for porous elastoplastic, damage and creep materials, as well as advanced formulations to represent fractures considering geomechanical effects.
Combined, this physics support can be used to solve several problems such as Reservoir compaction, Fault reactivation, Modelling of flow corridors, Well stability analysis, Naturally fractured reservoirs, Hydraulic fracturing, Reactive transport and many more.
GeMA includes several formulations for fracture modeling, considering the explicit and implicit representation of discontinuities.
GeMA includes several formulations for fracture modeling, considering the explicit and implicit representation of discontinuities. Some of these formulations are interface elements, extended finite elements, embedded fracture models, and dual-porosity/dual-permeability models. It allows modeling geomechanical problems, such as multistage hydraulic fracturing, fault reactivation, and fluid migration through highly fractured reservoirs, considering fractures in multiple scales and multiphysics coupling effects.
GeMA does not dictate how multiple physics are coupled. Those decisions can be made by engineers according to the scenario at hand.
GeMA does not dictate how multiple physics are coupled. Those decisions can be made by engineers according to the scenario at hand. Physics coupling can be either strong (fully coupled), where all relevant physics equations are combined in a single equation system, or weak (loosely coupled), where each physics is solved individually with their interaction effects modeled by several possible user-defined coupling strategies (1-way, 2-way, etc), as defined by the simulation orchestration script.
GeMA supports models featuring multiple domain discretizations (meshes) that can be used to simulate each physics process at its appropriate spatial and time scale.
GeMA supports models featuring multiple domain discretizations (meshes) that can be used to simulate each physics process at its appropriate spatial and time scale. Data can be transferred between these distinct domains at the desired simulation steps. Several interpolation techniques, both meshfree and mesh-aware, can be used for transferring data with minimum error.
Although most GeMA simulations are based on the Finite Elements Method, the framework is discretization method agnostic and supports other paradigms...
Although most GeMA simulations are based on the Finite Elements Method, the framework is discretization method agnostic and supports other paradigms that can be made available with additional plugins, in the same way as the FEM model is implemented. Some exercises have already been done with finite differences and discrete element methods
In a GeMA simulation, the orchestration script defines the applied solution method, or how we combine the available processes to simulate the given model.
In a GeMA simulation, the orchestration script defines the applied solution method, or how we combine the available processes to simulate the given model. This script is written in Lua, an interpreted language specially built to be embedded into applications, allowing them to dynamically run user-provided programs. It is considered a simple, easy-to-learn language that includes some powerful concepts and is also seen as one of the fastest available interpreted languages.
At the orchestration script, the user has access to all of the simulation data and is able to perform complex initializations, combine existing simulation methods with user-given calculations, define the coupling strategy for loosely coupled multiphysics simulations, define the steps where data should be transferred between meshes or written to disk, or even perform integration steps with external simulators.
The GeMA framework can combine finite element formulations with machine learning (ML) algorithms to improve or accelerate some processes
The GeMA framework can combine finite element formulations with machine learning (ML) algorithms to improve or accelerate some processes. The ML algorithms generate an approximated model of the nonlinear behavior of constitutive models or element formulations, drastically reducing the need for numerical iterations. The finite element method based on machine learning algorithms is used to estimate chemical reactions and fluid flow in porous media. The numerical results indicate that this approach can considerably reduce the error of the method and the computational cost of producing and solving the model.
The GeMA architecture is based on well-defined interfaces, together with plugins implementing those interfaces to provide the application with its modeling capabilities.
The GeMA architecture is based on well-defined interfaces, together with plugins implementing those interfaces to provide the application with its modeling capabilities. Plug-ins range from the mesh implementation to the available modeling processes and physics tied to them
This architecture, combined with the configurable orchestration, is the base for the framework's extensibility. Using plugins implementing well-defined interfaces also guarantees a high degree of modularization and uncoupling between system modules, features that, together with a strong set of regression tests, are crucial for creating an environment capable of evolving without decreasing its long time reliability.
GeMA simulations can be integrated with external simulators in two distinct ways.
GeMA simulations can be integrated with external simulators in two distinct ways. In the first one, the external simulator is seen as a black box and data is transferred between GeMA and the simulator by way of auxiliary files, written in the simulator’s own format. Those transfers are usually timed and executed by the orchestration script itself, together with data transfer between meshes when needed. For simulators that include a public API, the coupling can be done more efficiently at the process or physics plugin levels.
The black-box method has been successfully used for integration with the industry standard IMEX black oil reservoir simulator and with the GeoFlux3D simulator. The API method is used by the reactive transport physics plugin to integrate with the Phreeqc simulator.
A GeMA simulation model can include multiple user-defined functions. Written in Lua, those functions can be used to create additional node, cell, or integration point data, as well as provide dynamic values...
A GeMA simulation model can include multiple user-defined functions. Written in Lua, those functions can be used to create additional node, cell, or integration point data, as well as provide dynamic values for boundary conditions and user materials whose properties depend on the simulation state.
Alternative material laws can also be defined in the model, being an excellent choice for studying possible future material implementations.
The GeMA framework can take snapshots of the simulation state at user-defined steps in the orchestration script.
The GeMA framework can take snapshots of the simulation state at user-defined steps in the orchestration script. In the event of an unexpected failure, or if the simulation was interrupted by the user, those snapshots can be used to later resume the simulation at the saved step, without the need to restart the whole simulation.
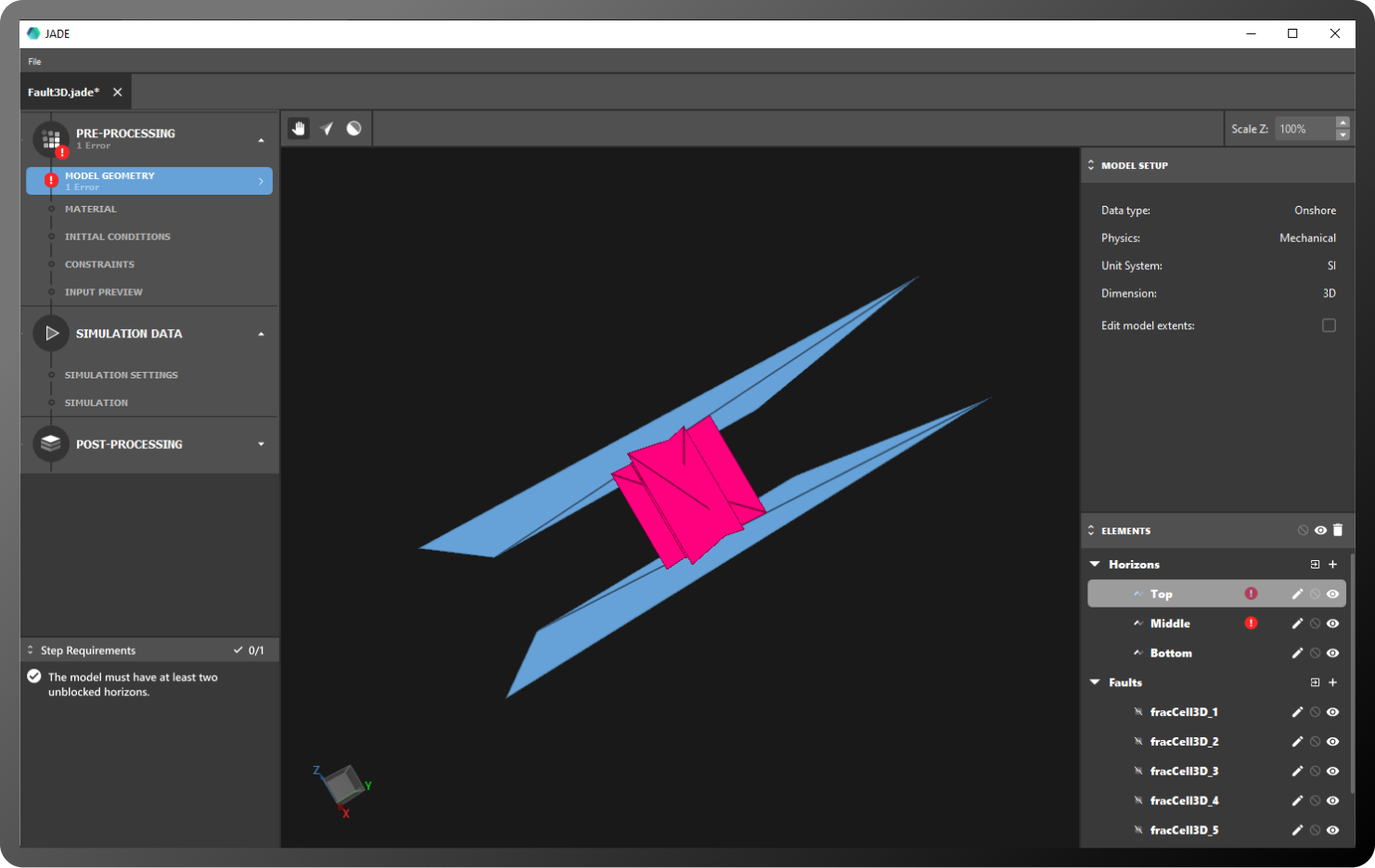
Building complex simulation models by hand, which includes defining meshes, boundary conditions, material properties, the orchestration script, etc., can be a time-consuming task. The Jade analysis and design environment can be used for effortlessly creating GeMA simulation models based on pre-defined templates. The generated models include everything needed to execute a GeMA simulation, from complex meshes created by importing layer surfaces, passing through several types of well-data-driven boundary conditions to the orchestration scripts for different simulation scenarios.
This benchmark shows the fluid flow migration in highly fractured formations with strong and small-interconnected fractures. The formulation uses concepts of dual domains and embedded fracture models. The effect of individual fractures is considered by adopting a homogenized permeability and a modified shape factor with data about their geometric location. The main advantage of this new method is the possibility of using regular meshes without the need to conform them to fractures. The results are compared against DFM using interface elements with excellent agreement. The hybrid approach accurately describes the pore pressure fields in formations with a considerable number of multiscale fractures.
This benchmark considers a fluid-driven fracture propagation in a permeable poroelastic formation. We implemented a zero-thickness triple-nodded interface element to represent the fracture and poroelastic solid elements for the permeable rock formation. The cohesive zone model governs the fracture propagation, and the fluid flow inside the fracture follows the cubic law of parallel plate. A fully coupled approach is adopted to solve the hydro-mechanical equation. The numerical simulation was performed using our in-house simulator called “GeMA”. The numerical solutions are compared with those obtained using analytic solutions in the toughness/storage dominated propagation regime. This validation of the hydraulic fracturing benchmark using GeMA shows its capability to simulate hydraulic fracturing applications for oil/gas industry.
This example investigates multistage hydraulic fracturing using a coupled HM Extended Finite Element Method (XFEM). Several vertical non-planar fluid-driven fractures are induced simultaneously to investigate the stress shadowing effects on the required pressure for crack propagation and on the resulting fracture geometry. Our numerical results also exhibit good agreement to asymptotic analytical solutions for fracture propagation in single and multi-layered formations under homogeneous and heterogeneous stress conditions.
Salt rocks exhibit time-dependent strain behavior when submitted to deviatoric stresses. This behavior is described by creep constitutive laws based on deformation mechanics. One of the major challenges in modeling stress states in sedimentary basins in the presence of salt structures is to predict the magnitude of stress perturbations around salt bodies. Modeling is driven by the fact that salt bodies cannot sustain deviatoric stresses. Therefore, the final stress state is affected by relaxing stresses within the salt body, causing load transfer to the adjacent formation until the stress redistribution reaches the steady state condition and the deviatory stress within the salt body decays to nearly zero.
This section presents an application of flow and transport through a realistic porous medium. The pore dimensions are compatible with a hydrocarbon reservoir. The numerical model consists of a rectangular blade crossing non-regular shaped grains of the porous medium. The grain contours derive from SEM images and a *.dxf file is available on the website of the software COMSOL Multiphysics. The grain contours file has been imported and worked over using a pre-processor, and the model has been run in GeMA framework. Contour maps of the velocity magnitude and of the concentration evolution over time are shown. These results are useful to estimate the average permeability and to analyze the evolution of the flow and transport over the porous medium.
This section presents an application of creep and interlayer slippage behaviors in a salt cavern. The scenario is based on the Room D of the Waste Isolation Pilot Plant (WIPP), an underground repository in USA. The galleries were excavated in a formation composed of intercalations of salt with argillaceous salt, anhydrite, polyhalite and clay seams. A layered model has been built in a pre-processor. Interface elements have been adopted to represent the clay seams. The model has been run in GeMA framework. Contour maps of the displacement magnitude and the mesh deformation are shown. These results are useful to identify problematic zones in terms of serviceability and mechanical integrity.
Alternatively, the GeMA application can also be installed by just copying the contents of the zip file to a folder of choice.
PHD. THESIS, PUC-RJ, 2016.
MENDES, C.A.T.
PROCEEDINGS OF THE VII EUROPEAN CONGRESS ON COMPUTATIONAL METHODS IN APPLIED SCIENCES AND ENGINEERING, ECCOMAS CONGRESS 2016.
MENDES, C.A.T. ; GATTASS, M. ; ROEHL, D.