 |
DGFemPhysics
The GeMA Discontinuous Galerkin FEM Physics Plugin
|
 |
DGFemPhysics
The GeMA Discontinuous Galerkin FEM Physics Plugin
|
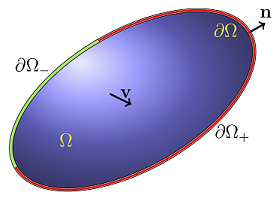
Discontinuous Galerkin (DG) methods can be viewed as finite element method allowing for discontinuities in the discrete trial and test spaces. From a practical viewpoint, working with discontinuities discrete spaces leads to compact discretization stencil and, at the same time, offers a substantial amount of flexibility, making the approach appealing for multi-domain and multiphysics simulations. Let a unsteady version of advection-reaction boundary condition problem, for a given finite time \(t_f>0\), consider the time evolution problem:
\begin{eqnarray*} \phi\frac{\partial c}{\partial t} + \mathbf{v}\cdot \text{grad}{(c)} + R = f & \text{in} & \Omega \times (0,t_f)\\ c = c_{\text{in}} & \text{on} & \partial \Omega_{-} \times (0,t_f)\\ c(\cdot , t = 0) = c_0 & \text{in} & \Omega \end{eqnarray*}
with porosity \(\phi\), advective velocity \(\mathbf{v}\), reaction term \(R\), source term \(f\), inflow value \(c_{\text{in}}\), and initial datum \(c_0\). Is it import recall that \(\partial \Omega_{-} := \left\{ x \in \partial \Omega \,|\, \mathbf{v} \cdot \mathbf{n}(x) < 0 \right\}\) where \(\partial \Omega\) represent the boundary of bound domain \(\Omega\subset \mathit{R}^{n}\) with \( n=1,2,3\). Here, the unknown function \(c:=c(x,t)\) is a scalar-valued and represents, e.g., a solute concentration.
Using the notation and concepts presented in Mathematical Aspects of Discontinuities Galerkin Methods of Daniele Di Pietro and Alexandre Ern, the discret variational form of advective-reactive problem is:
Let \(T_h\) be a regular family decomposition of \(\Omega\) into regular quadrilateral/hexahedral elements \(K\) such that \(\bigcup _{K \in T_h} K = \Omega_h \subseteq \Omega \) and given local order approximation \(p\geq 1\), find \(c_h\in C_h^p\) such that
\[ a_h(c_h,\psi) + a_\Gamma(c_h,\psi) = b_f(\psi) + b_{\text{in}}(\psi) \quad \forall \psi \in C_h^p \]
where
\[ a_h (c_h,\psi) := \sum_{K\in T_h} \int_K \left[\psi\,\phi\,\frac{\partial c}{\partial t}{-c}_h\, \mathbf v \cdot \text{grad}( \psi) + R \psi \right] dx \, , \qquad a_{\Gamma}(c_h,\psi) := \sum_{K\in T_h}\int_{\partial K} [\!| \psi |\!] \cdot \{\!|c_h \, \mathbf v|\!\}_{\text {u}} ds + \int_{\partial\Omega_+} c_h \, \mathbf v \cdot \mathbf n \, \psi ds\, , \]
\[ b_f(\psi) := \sum_{K\in T_h}\int_{K} f \, \psi \, dx \, , \qquad b_{\text{in}}(\psi) := -\int_{\partial\Omega_{-}} c_{\text{in}} \, \mathbf{v} \cdot \mathbf{n} \psi \, ds\, , \]
and
\[ C_h^p:= \left\{ c_h \in L^2(\Omega_h) \; | \; c_h\big|_K\in \mathrm{Q}_p(K) , \; \forall K \in T_h \right\} \, . \]
The above variational form is stable, but only in \(L^2(\Omega)\)-norm. The practical consequence of this can be detrimental : discontinuities in the boundary or initial datum may trigger large, non-physical oscillations in the numerical solution. In the order to design a formulation that is stable in a stronger norm, on every internal edge \(\partial K\), common to the elements \(K_1\) and \(K_2\) the upwind value of \((c\,\mathbf{v})\) is defined as:
\[ \{\!| c_h \, \mathbf v|\!\}_{\text{u}}= \left\{ \begin{array}{ccc} c_h^1 \, \mathbf{v} & \text{if} & \mathbf{v} \cdot \mathbf{n}> 0 \, , \\ c_h^2 \, \mathbf{v} & \text{if} & \mathbf{v} \cdot \mathbf{n}< 0 \, , \\ \{\!| c_h |\!\} \, \mathbf{v} & \text{if} & \mathbf{v} \cdot \mathbf{n}= 0 \, . \\ \end{array} \right. \qquad\text{(Upwind Flux)} \]
The use of a reference element, and therefore of coordinate changes, is a essential ingredient of finite element methods. Let \(\hat{K}\subset R^{n}\) and \(F\) a smooth mapping of \(R^n\) into \(R^n\), we defined \(K = F(\hat{K})\) for all \(K \in T_h\) such that for \(p\geq 1\), \( Q_p(K) := \hat{Q}_p(F^{-1}(K)) \) where
\[ \hat{Q}_p (\hat{K}):= \left\{\xi_1^i \xi_2^j\, ; \; (\xi_1,\xi_2)\in \hat{K}=[-1,1]^2\;\; \big|\;\; i,j = 0,\dots,p\right\}\quad \text{for quadrilateral elements and } \hat{Q}_p (\hat{K}):= \left\{\xi_1^i \xi_2^j\xi_3^k\, ; \; (\xi_1,\xi_2,\xi_3)\in \hat{K}=[-1,1]^3\;\; \big|\;\; i,j,k = 0,\dots,p\right\} \quad \text{ for hexahedral elements.} \]
A reference manual documenting the set of state variables and material properties expected by the plugin, along with all of its supported configuration and result options can be found here.
 1.8.15
1.8.15