Interface elements

Introduction

To be implemented ...

Formulation

The weak form of the equilibrium equation, including the interface effects, follow from the principle of virtual work. The virtual work done by the body forces \((b)\) in the domain \(\Omega\) and by the external traction \((T_{ex})\) on the boundary \(\Gamma\) are equal to the sum of the virtual strain energy in the domain \(\Omega\) and the cohesive fracture energy on the fracture surface \(\Gamma\).

Figure 1: Schematic representation of a domain with an internal fracture

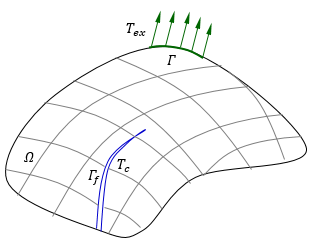
\[ \int_\Omega \delta\epsilon:\sigma d\Omega + \int_{\Gamma} \delta\Delta:T_c d\Gamma =\int_{\Omega} \delta u:b d\Omega + \int_{\Gamma} \delta u:T_{ex} d\Gamma \]

where:

• \( \delta\epsilon \) is the virtual strains
• \( \delta u \) is the virtual displacements
• \( \delta\Delta \) is the virtual fracture opening
• \( T_c \) is the cohesive tractions

Following the standard finite element procedures (Zienkiewicz, 1980; Potts and Zdravkovic, 1999), the internal force vector \((F_c)\) of an interface element is given by

\[ F_c = \int_\Gamma B_c^T T_c d\Gamma \]

The gradient of the internal force vector leads to the tangent matrix of the interface element,

\[ K_c = \int_\Gamma B_c^T D_c B_c d\Gamma \]

where \(D_c = \partial T_c / \partial\Delta\) is the constitutive matrix relating tractions and relative displacements on the fracture surface.

Plugin options

Mechanical interface element supports the plugin options detailed in Mechanical Fem Plugin options and additional plugin options only for interface elements are detailed below:

Plugin object types

The mechanical interface plugin only publishes one object type and so references to the plugin name while creating a physics object requires the type name.

a) Objects type for interface elements

• Interface

Example:

PhysicalMethod {
  id       = 'cohesive',
  typeName = 'MechanicalFemPhysics.Interface',
  type     = 'fem',

  mesh = 'mesh',
  materials = {'cohesiveExponentialSoftening'},
  ruleSet = 1,
  boundaryConditions = {'bc1', 'bc2'}, 
}

State variables

The Continuum element plugin requires the model to contain the displacement state variable 'u', which is a vector with size equal to the node coordinate dimension. Further details see: Mechanical state variables.

Material types

The mechanical interface element supports several materials as detailed below:

Material type	Material name
Elastic Interface	elasticInterface
Cohesive Linear Softening	cohesiveLinearSoftening
Cohesive Exponential Softening	cohesiveExponentialSoftening
Interface Mohr Coulomb	interfaceMohrCoulomb

The mechanical interface materials are fully described in Interface material reference.

Physics attributes

When defining plugin object of Mechanical fem Physic, the following fields are available for usage during the definition:

Attribute	Description	Type	Required	Def. Value
id	The physics name.	String	Yes	-
	Example: id = 'myPhysicsName'
typeName	Physics defines the plugin name according to the type name such as 'planeStress','planeStrain', etc.	String	Yes	-
	Example: typeName = 'MechanicalFemPhysics.3D'
type	Type of physics object. Should be equal to 'fem'.	String	Yes	-
	Required value: type= 'fem'
ruleSet	Integration rule set selected for simulation elements.	String	No	Empty
	Example: ruleSet = 1

Like other Fem physics, stateVar, property and attribute renaming fields are supported. Likewise, restricting the physics application domain to a set of cell groups, setting the desired integration rule and unit system remapping are also available. Those common optional fields are detailed at the GeMA Common Fem Porocess.

Example for problems using Interface Elements:

PhysicalMethod {
  id       = 'Fracture',
  typeName = 'MechanicalFemPhysics.Interface',
  type     = 'fem',
  mesh     = 'mesh',
  ruleSet  = 1, 
  boundaryConditions = {'bc1','bc2','bc4','bc5','bc6'},
  materials = {'elasticInterface','cohesiveLinearSoftening'},
}

Boundary conditions

The Interface element plugin supports the Boundary condititons detailed in Mechanical Boundary Conditions.

Supported elements

The Mechanical Fem physics supports 2D and 3D elements. Supported elements are:

• int2dl4
• int3dl8
• int3dl6

Unit system

The Mechanical Fem physics uses internally the international system of units for its calculations, as can be seen above by the default units for properties and attributes. The whole unit system can be replaced through the unitSystem physics attribute, as described at the gemaFemProcessCommonFemPhysicsOptions page.

When making the substitution, the units on the follwoing table should be replaced by the desired units, forming a coherent unit system. The unit system of the material should be also replaced.

local newUnitSystem = {
  time     = 's',
  coord    = 'm',
  u        = 'm',
  F        = 'kN',
  E        = 'kPa',
  pressure = 'kPa',
  Sws      = 'kN/m3',
  gr       = 'm/2',
  pl       = 'kPa',
}

References

1.Potts, D. M. and Zdravkovic, L. (1999). Finite elements analysis in geotechnical engineering - Theory. 68-70. Thomas Telford.

2.Zienkiewicz OC. (1980). Finite element methods. Editiorial Reverte: Barcelona.

GeMA project main page