 |
MechanicalFemPhysics
The GeMA Mechanical FEM Physics Plugin
|
 |
MechanicalFemPhysics
The GeMA Mechanical FEM Physics Plugin
|
The Solidifying Kelvin Chain material considers the Solidification Theory proposed by Bažant and Prasannan [1] applied in Kelvin chains to represent the basic creep of concrete. In this way, aging is modeled as a growth of the volume fraction of load-bearing solidified matter (hydrated cement), which itself is treated as nonaging viscoelastic material. For illustrative purposes, Figure 1 shows the role of solidification in creep.
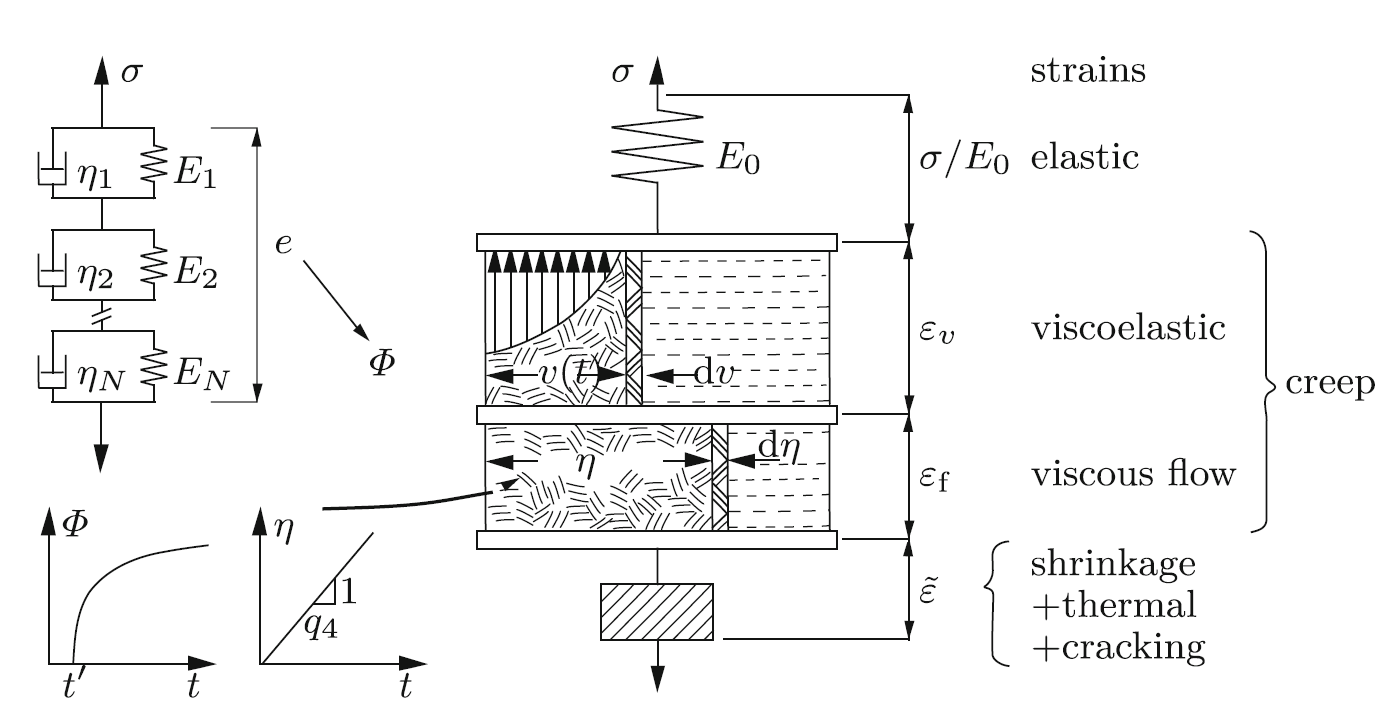
For the linear range of creep, the Boltzmann superposition principle is valid. Consequently, the basic creep can be characterized by the compliance function \( J \) and the strain \( \varepsilon \) can be written in terms of the increment of stress \( d\sigma \):
\[\begin{matrix} \varepsilon \left( t \right)=\int_{0}^{t}{J\left( t,{t}' \right)d\sigma \left( {{t}'} \right)} & \left( 1 \right) \\ \end{matrix}\]
where \(t\) is the current time and \({t}'\) is the time application of \(d\sigma \). Differentiating \(\left( 1 \right)\) according to the Leibniz rule, we have
\[\begin{matrix} \dot{\varepsilon }\left( t \right)=J\left( t,t \right)\dot{\sigma }\left( t \right)+\int_{0}^{t}{\dot{J}\left( t,{t}' \right)d\sigma \left( {{t}'} \right)} & \left( 2 \right) \\ \end{matrix}\]
where the dot over \(J\) denotes the partial derivative with respect to \(t\). Observe that equations \(\left( 1 \right)\) and \(\left( 2 \right)\) are suitable for aging materials, once \(J\) is a function of two variables.
In the solidification theory, the aging is attributed to the volume growth of C-S-H gel, treated as a substance of time-invariant properties. The specific volume of cement gel that has solidified up to time \(t\) is denoted as \(v\left( t \right)\). The contribution of stress-strain increment is proportional to specific volume growth and equation \(\left( 2 \right)\) is rewritten as
\[\begin{matrix} \dot{\varepsilon }\left( t \right)=\frac{1}{v\left( t \right)}\left[ \Phi \left( 0 \right)\dot{\sigma }\left( t \right)+\int_{0}^{t}{\dot{\Phi }\left( t-{t}' \right)d\sigma \left( {{t}'} \right)} \right] & \left( 3 \right) \\ \end{matrix}\]
where \(\Phi \left( t-{t}' \right)\) is the nonaging compliance function of the cement gel. For the solidification effect, it is used an experimentally justified function from the double-power law and log-double-power law:
\[\begin{matrix} \frac{1}{v\left( t \right)}={{\left( \frac{{{\lambda }_{0}}}{t} \right)}^{m}}\frac{1}{\alpha }+1 & \left( 4 \right) \\ \end{matrix}\]
where \({{\lambda }_{0}}\), \(m\) and \(\alpha \) are empirical constants. Since for most concretes one can use the approximate values \({{\lambda }_{0}}=1\) day and \(m=0.5\), these values are fixed in GeMA.
To represent the compliance function \(\Phi \left( t-{t}' \right)\), it is used a Kelvin Chain, shown in a general scheme in Figure 2.
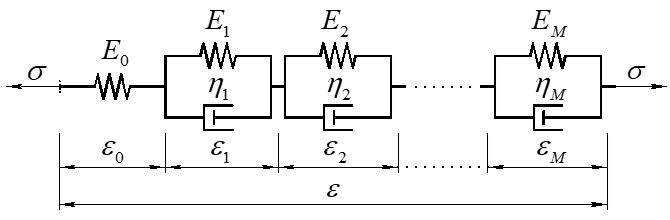
Considering the assumption that the evolution of properties is given by \({{E}_{i}}\left( t \right)=v\left( t \right)E_{i}^{\left( \infty \right)}\) and \({{\eta }_{i}}\left( t \right)=v\left( t \right)\eta _{i}^{\left( \infty \right)}\), the compliance function of a Kelvin Chain composed of M+1 units with asymptotic elastic moduli \(E_{i}^{\left( \infty \right)}\), \(i=0,\text{ }1,\text{ }2\text{ }...\text{ }M\) and asymptotic viscosities \(\eta _{i}^{\left( \infty \right)}\), \(i=1,\,\,2\,\,\ldots M\) can be written as
\[\begin{matrix} \Phi \left( t-{t}' \right)=\left[ \frac{1}{E_{0}^{\left( \infty \right)}}+\sum\limits_{i=1}^{M}{\frac{1}{E_{i}^{\left( \infty \right)}}\left( 1-{{\text{e}}^{{-\left( t-{t}' \right)}/{{{\tau }_{i}}}\;}} \right)} \right]H\left( t-{t}' \right) & \left( 5 \right) \\ \end{matrix}\]
where \({{\tau }_{i}}={\eta _{i}^{\left( \infty \right)}}/{E_{i}^{\left( \infty \right)}}\;\)are the retardation times. From the mathematical point of view, the time-dependent part of \(\left( 5 \right)\) is the Dirichlet series (or Prony series) [2].
By solving the integral semi analytically assuming exponential series for the compliance and linear stress variation in each increment [3, 4], the strains given in equation \(\left( 3 \right)\) can be calculated with implicit integration. Considering an increment of time \(\Delta t={{t}_{n+1}}-{{t}_{n}}\), the corresponding increment of strain is
\[\begin{matrix} \Delta \varepsilon =\frac{1}{v\left( {{t}^{*}} \right)}\left\{ \frac{{{\sigma }_{n+1}}-{{\sigma }_{n}}}{E_{0}^{\left( \infty \right)}}+\sum\limits_{i=1}^{M}{\left[ \varepsilon _{i,n}^{ve}\left( {{\text{e}}^{{-\Delta t}/{{{\tau }_{i}}}\;}}-1 \right)+\frac{{{\sigma }_{n}}}{E_{i}^{\left( \infty \right)}}{{f}_{n}}\left( {\Delta t}/{{{\tau }_{i}}}\; \right)+\frac{{{\sigma }_{n+1}}}{E_{i}^{\left( \infty \right)}}{{f}_{n+1}}\left( {\Delta t}/{{{\tau }_{i}}}\; \right) \right]} \right\} & \left( 6 \right) \\ \end{matrix}\]
where \(\varepsilon _{i,n}^{ve}\) is the viscoelastic strain in the i-th element of Kelvin chain in the instant \({{t}_{n}}\), and \({{\sigma }_{n}}\) and \({{\sigma }_{n+1}}\) are, respectively, stresses in times \({{t}_{n}}\) and \({{t}_{n+1}}\). The functions \({{f}_{n}}\) and \({{f}_{n+1}}\) are derived from numerical integration and have the following form:
\[\begin{matrix} {{f}_{n+1}}\left( \xi \right)=1-\frac{1}{\xi }\left( 1-{{\text{e}}^{-\xi }} \right) & \left( 7 \right) \\ \end{matrix}\]
\[\begin{matrix} {{f}_{n}}\left( \xi \right)=1-{{\text{e}}^{-\xi }}-{{f}_{n+1}}\left( \xi \right) & \left( 8 \right) \\ \end{matrix}\]
For the multiaxial approach, the compliance function is obtained by appropriate scaling of uniaxial compliance, assuming that Poisson`s ratio is not affected by creep and can be considered as a constant [5]. Thus, equation \(\left( 6 \right)\) can be written as follows:
\[\begin{matrix} \Delta \mathbf{\varepsilon }=\frac{1}{v\left( {{t}^{*}} \right)}\left\{ {{\mathbf{C}}_{\nu }}\frac{{{\mathbf{\sigma }}_{n+1}}-{{\mathbf{\sigma }}_{n}}}{{{E}_{0}}}+\sum\limits_{i=1}^{M}{\left[ \mathbf{\varepsilon }_{i,n}^{ve}\left( {{\text{e}}^{{-\Delta t}/{{{\tau }_{i}}}\;}}-1 \right)+{{\mathbf{C}}_{\nu }}\frac{{{\mathbf{\sigma }}_{n}}}{{{E}_{i}}}{{f}_{n}}\left( {\Delta t}/{{{\tau }_{i}}}\; \right)+{{\mathbf{C}}_{\nu }}\frac{{{\mathbf{\sigma }}_{n+1}}}{{{E}_{i}}}{{f}_{n+1}}\left( {\Delta t}/{{{\tau }_{i}}}\; \right) \right]} \right\} & \left( 9 \right) \\ \end{matrix}\]
where \({{t}^{*}}={{t}_{n}}+{\Delta t}/{2}\;\), \(\mathbf{\sigma }\) and \(\mathbf{\varepsilon }\) are, respectively, the stress and the strain tensors in the Voight notation, and \({{\mathbf{C}}_{\nu }}\) is the dimensionless elastic compliance matrix corresponding to a unit value of Young`s modulus, given by
\[\begin{matrix} {{\mathbf{C}}_{\nu }}=\left[ \begin{matrix} 1 & -\nu & -\nu & 0 & 0 & 0 \\ -\nu & 1 & -\nu & 0 & 0 & 0 \\ -\nu & -\nu & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2\left( 1+\nu \right) & 0 & 0 \\ 0 & 0 & 0 & 0 & 2\left( 1+\nu \right) & 0 \\ 0 & 0 & 0 & 0 & 0 & 2\left( 1+\nu \right) \\ \end{matrix} \right] & \left( 10 \right) \\ \end{matrix}\]
The viscoelastic tangent consistent operator \({{\mathbf{D}}^{ve}}\) is defined by the relation \({\Delta \mathbf{\sigma }}/{\Delta \mathbf{\varepsilon }}\;\), and has the form
\[\begin{matrix} {{\mathbf{D}}^{ve}}=v\left( {{t}^{*}} \right){{\left( \frac{1}{{{E}_{0}}}+\sum\limits_{i=1}^{M}{\frac{{{f}_{n+1}}\left( {\Delta t}/{{{\tau }_{i}}}\; \right)}{{{E}_{i}}}} \right)}^{-1}}{{\mathbf{D}}_{\nu }} & \left( 11 \right) \\ \end{matrix}\]
where \({{\mathbf{D}}_{\nu }}=\mathbf{C}_{\nu }^{-1}\) is the dimensionless elastic stiffness matrix, corresponding to a unit value of Young`s modulus. Two-dimensional versions of the stress-strain law valid under plane-stress or plane-strain conditions are easily obtained by an appropriate modification of matrices \({{\mathbf{C}}_{\nu }}\) and \({{\mathbf{D}}_{\nu }}\).
The Solidifying Kelvin Chain material requires the following properties:
| Property | Description | Type | Def. Unit | Required |
|---|---|---|---|---|
| E0 | Elastic modulus of outer spring | Scalar | kPa | Yes |
| nu | Poisson`s ratio | Scalar | – | Yes |
| Ei | Elastic moduli of Kelvin chain | Scalar /vector | kPa | Yes |
| tau | Retardation times of Kelvin chain | Scalar /vector | day | Yes |
| alpha (*) | Aging alpha factor | Scalar | – | Yes |
(*) If alpha is declared equal to zero, \({1}/{v\left( t \right)}\;\) will be considered equal to one, and, consequently, the material will not have aging.
Example: Solidifying Kelvin chain with three elements calibrated from experimental data available in Saliba, Grondin [6].
User must set in *_solution.lua file the physical method to activate the solidifying Kelvin chain material. It is possible also to set the models under plane stress or plane stress conditions.
Example:
1. Bažant, Z.P. and S. Prasannan, Solidification theory for aging creep. Cement and Concrete Research, 1988. 18(2): p. 923-932.
2. Bažant, Z.P. and S.T. Wu, Dirichlet series creep function for aging concrete. Journal of Engineering Mechanics - ASCE, 1973. 99(EM2): p. 367-387.
3. Dias, F.C., Análise viscoelástica de estruturas de concreto sujeitas a envelhecimento e dano do material, in Departamento de Engenharia Civil e Ambiental. 2020, Pontifícia Universidade Católica do Rio de Janeiro: Rio de Janeiro. p. 110.
4. Brandão, N.B., et al., The impact of cement slurry aging creep on the construction process of oil wells. Journal of Petroleum Science and Engineering, 2017. 157: p. 422-429.
5. Bažant, Z.P., Continuous retardation spectrum for solidification theory of concrete creep. Journal of Engineering Mechanics, 1995. 121: p. 281-288.
6. Saliba, J., et al., Numerical Investigation of the Size Effects on the Creep Damage Coupling. Procedia Materials Science, 2014. 3: p. 1038-1043.
Returns to Mechanical continuum material.
 1.8.15
1.8.15