Introduction

The Thermo FEM physics plugin is responsible for providing an implementation for the heat equation that can be used together with the Fem process to solve steady state and transient heat conduction problems, both in 2D and 3D. The current implementation does not include a convective transport term. The main equation solved by this physics is:

\[ \rho c_p \frac{\partial T}{\partial t} = \nabla\cdot(\lambda \nabla T) + G \]

where:

\(T\) is the temperature in \(K\)
\(t\) is the time in \(s\)
\(\rho\) is the density in \(kg/m^3\)
\(c_p\) is the specific heat capacity at constant pressure in \(J/(kg.K)\)
\(\lambda\) is the heat conductivity tensor in \(W/(m.K)\)
\(G\) is a heat generation term per unit volume in \(W/m^3\)

Both Dirichlet (prescribed temperatures) and Neumann (prescribed heat fluxes) boundary conditions can be prescribed on model borders. Adiabatic conditions are modeled with a no flow condition \(q_0 = 0\), where \(q_0\) is the heat flux in \(W/m^2\). Convective heat transfers at the borders are modeled with a heat flux given by \(q_0 = h(T - T_a)\), where \(h\) is the convection coefficient, in \(W/(m^2.K)\), and \(T_a\) is the ambient temperature. The available conditions are sumarized by the following set of equations:

\begin{eqnarray*} T = T_0 &~~ \textrm{in} & \Gamma_d\\[2ex] -\lambda \frac{\partial T}{\partial n} = q_0 &~~ \textrm{in} & \Gamma_{n1}\\[2ex] -\lambda \frac{\partial T}{\partial n} = h(T - T_a) &~~ \textrm{in} & \Gamma_{n2} \end{eqnarray*}

Boundary conditions for the heat equation.

Formulation Reference

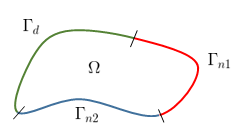
The FEM discretization of the heat equation used by the Thermo Fem physics plugin is based on the book Fundamentals of the Finite Element Method for Heat and Fluid Flow by Roland W. Lewis, Perumal Nithiarasu and Kankanhalli N. Seetharamu, 2004.

Plugin options

A reference manual documenting the set of state variables and material properties expected by the plugin, along with all of its supported configuration and result options can be found here.

Examples

Several example simulations involving both linear and non-linear, steady state and transient temperature calculations are available at the examples directory provided with the GeMA instalation. A summary of those examples can be found here.

GeMA project main page