Throughout this tutorial, most examples will be based on a simple heat conduction scenario. Consider a simple 2D square plate as shown in Figure 5. Its top border has a fixed temperature of 500 degrees Celsius, while the other three sides have a fixed temperature of 100 degrees Celsius. The plate's heat conductivity is equal to 10 W/(m.K).

Figure 5: Sample heat conduction example.

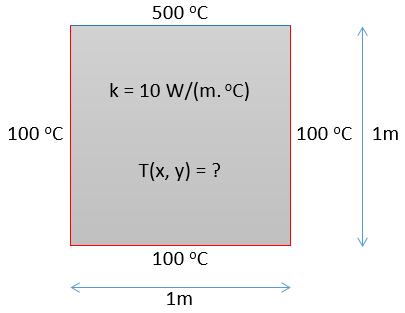
The first analyzed problem will be a simple steady state heat conduction problem where the user wants to know the temperature distribution on the plate, according to the given boundary conditions. To solve this problem, the plate domain will be discretized in triangles and the temperature equation solved by the finite element method. It has an analytical solution that can be used for validation given by:

\[ T(x, y) = T_{side} + (T_{top} - T_{side})\frac{2}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{n+1} + 1}{n} \sin\left(\frac{n \pi x}{w}\right) \frac{\sinh\left(\mbox{$\frac{n\pi y}{w}$}\right)}{\sinh\left(\mbox{$\frac{n\pi h}{w}$}\right)} \]

where w and h are, respectively, the plate's width and height. This problem corresponds to example 5.2.1 given in the book "Fundamentals of the Finite Element Method for Heat and Fluid Flow", by Lewis et al.

The second problem, corresponding to example 6.6.1 from the same book, analyzes the transient problem when the same boundary conditions are suddenly imposed over a plate with an initial uniform temperature equal to 0 degrees Celsius. The material density is equal to 2 kg/m3 and its specific heat capacity is equal to 10 J/(kg.K).

A multi-physics problem combining heat conduction with stress analysis will be presented on section VIII - Multi-physics example.

Go to the next section, previous section or return to the index