Shape function handling base classe. More...

#include <gmShape.h>

Inheritance diagram for GmShape:

[legend]

Collaboration diagram for GmShape:

[legend]

Public Member Functions
virtual GmCellType	elemType () const =0
	Returns the type of this element.

virtual int	numFunctions () const =0
	Returns the number of shape functions of this element type (equal to the number of nodes)

virtual int	numNaturalCoord () const =0
	Returns the number of natural coordinates used by this element type.

virtual int	numCartesianCoord () const =0
	Returns the number of cartesian coordinates expected by this element type.

virtual void	naturalCoordLimits (int coord, double min, double max) const =0
	Fills min and max with the domain limits for the given natural coordinate (between 0 and numNaturalCoord() - 1)

virtual void	nodeNaturalCoord (int node, GmVector &coord) const =0
	Fills the coord vector with the set of natural coordinates for the reference shape function node. Node should be a value between 0 and numFunctions(). This is generally equal to the number of nodes but can be different for interface elements. More...

virtual void	naturalCenter (GmVector &coord) const =0
	Fills the coord vector with the set of natural coordinates for the element center. More...

void	fillNaturalCoordinates (GmMatrix &coord, bool transposed=false) const
	Fills the coord matrix with the set of natural coordinates for the shape nodes. More...

virtual bool	translateEdgePoint (int edge, const GmVector &srcEdgeCoord, GmVector &elementCoord) const =0
	Given a "bar like" edge coordinate (from -1 to 1), at the given edge, fills elementCoord with the equivalent element natural coordinate. Should be implemented for 2D & 3D elements. More...

virtual bool	translateFacePoint (int face, const GmVector &srcFaceCoord, GmVector &elementCoord) const =0
	Given a "quad like" or "tri like" face coordinate (-1 to 1 pair for quad faces and 0 to 1 barycentric triple for tri faces), at the given face, fills elementCoord with the equivalent element natural coordinate. Should be implemented for 3D elements. More...

virtual bool	cartesianToNatural (const GmVector &coord, const GmMatrix &X, GmVector &ncoord, bool *inside) const
	Given a set of cartesian coordinates 'coord' and a matrix with node coordinates 'X', calculates the corresponding natural coordinate filling 'ncoord'. The inside parameter is filled with true if the given cartesian coordinate is inside the element, false otherwise. More...

virtual bool	cartesianToNatural (const GmVector &coord, const GmMatrix &X, bool preferGeometric, double gradTol, int maxGradIter, double outsideNatTol, GmVector &ncoord, bool *inside) const
	Given a set of cartesian coordinates 'coord' and a matrix with node coordinates 'X', calculates the corresponding natural coordinate filling 'ncoord'. The inside parameter is filled with true if the given cartesian coordinate is inside the element, false otherwise. More...

virtual void	naturalToCartesian (const GmVector &ncoord, const GmMatrix &X, GmVector &coord) const
	Given a set of natural coordinates 'ncoord' and a matrix with node coordinates 'X', calculates the corresponding cartesian coordinates filling 'coord'. More...

virtual void	shapeValues (const GmVector &ncoord, GmVector &N) const =0
	Function used to evaluate the set of shape functions over a point defined by its natural coordinates. More...

virtual void	shapePartials (const GmVector &ncoord, GmMatrix &dN, bool transposed=false) const =0
	Function used to calculate shape function partial derivatives with respect to its natural coordinates, evaluated at the given point. More...

virtual double	shapeCartesianPartialsFromCoord (const GmVector &ncoord, const GmMatrix &X, GmMatrix &dN, bool transposed=false) const
	Function used to calculate shape function partial derivatives with respect to its cartesian coordinates, evaluated at the given point. More...

virtual double	shapeCartesianPartialsFromJacobian (const GmVector &ncoord, const GmMatrix &J, GmMatrix &dN, bool transposed=false) const
	Alternative version of shapeCartesianPartials() to calculate shape function partial derivatives with respect to its cartesian coordinates, given a previously calculated Jacobian matrix. More...

virtual double	shapeCartesianPartialsFromPJ (const GmMatrix &P, const GmMatrix &J, GmMatrix &dN, bool transposed=false) const =0
	Alternative version of shapeCartesianPartialsXxxx() to calculate shape function partial derivatives with respect to its cartesian coordinates, given a previously calculated Jacobian matrix and a previously calculated shape function partial matrix. More...

virtual void	jacobian (const GmVector &ncoord, const GmMatrix &X, GmMatrix &J, bool transposed=false) const
	Calculates the jacobian matrix, relating cartesian coordinates to natural coordinates. More...

virtual double	scaledJacobianDet (const GmMatrix &J) const =0
	Returns the Jacobian determinant multiplied by the scaling factor needed for transforming the differential area element. dOmega = dx.dy = J.dXi.dEta where J is the scaled Jacobian determinant. More...

virtual void	jacobianAndPartials (const GmVector &ncoord, const GmMatrix &X, GmMatrix &J, GmMatrix &P, bool transposed=false) const =0
	This function does the same calculations as the jacobian() call, but also filling the extra parameter P with the matrix of shape function partials. More...

virtual double	borderScalingFactor (int border, const GmVector &borderCoord, const GmVector &elementCoord, const GmMatrix &X, bool transposed=false) const =0
	Returns the scaling factor needed when calculating integrals over borders (edges or faces). This has the same effect as the jacobian determinant when integrating over the whole element. It can be used to treat 2D and 3D edge / face boundary conditions in a single code. More...

virtual double	edgeScalingFactor (int border, const GmVector &borderCoord, const GmVector &elementCoord, const GmMatrix &X, bool transposed=false) const =0
	Returns the scaling factor needed when calculating integrals over element edges. This has the same effect as the jacobian determinant when integrating over the whole element. More...

virtual double	faceScalingFactor (int border, const GmVector &borderCoord, const GmVector &elementCoord, const GmMatrix &X, bool transposed=false) const =0
	Returns the scaling factor needed when calculating integrals over element faces. This has the same effect as the jacobian determinant when integrating over the whole element. More...

virtual const GmMatrix &	gaussExtrapolationMatrix (const GmIntegrationRule *ir) const
	Given an integration rule, compatible with the current element type, constructs an extrapolation matrix to calculate node values from integration point values. More...

virtual bool	pointExtrapolationMatrix (const GmMatrix &points, GmMatrix &em) const
	Given the set of 'm' natural coordinates in points, builds an 'n x m' extrapolation matrix that can be used to extrapolate values from an 'm' sized value vector to the 'n' elements nodes. More...

double	interpolate (const GmVector &nodeValues, const GmVector &ncoord) const
	Given a set of node values and a set of natural coordinates, interpolates the node values on the given coordinate. More...

Static Public Member Functions
static bool	initShapeFunctions ()
	Initializes the shape function module. Must be called BEFORE any calls to shapeFromElementType() or linearShapeFromElementType(), but AFTER the static initialization of the geometry objects. More...

static void	setConfigOptions (const GmSimulationData *simData)
	Updates the default config options used by the "simple" cartesianToNatural() call.

static const GmShape *	shapeFromElementType (GmCellType etype, int P, int Q)
	Returns a shape object suitable for handling elements of type etype. Parameters P and Q are needed only when working with hierarchical element types, such as GM_HQUADP or GM_HHEXP. They can be set to 0 for "common" element types.

static const GmShape *	linearShapeFromElementType (GmCellType etype, int P, int Q)
	Returns a linear shape object suitable for handling elements of type etype. Parameters P and Q are needed only when working with hierarchical element types, such as GM_HQUADP or GM_HHEXP. They can be set to 0 for "common" element types.

Protected Member Functions
virtual void	jacIndependentNatCoord (const GmVector &ncoord, const GmMatrix &X, GmMatrix &J, GmMatrix &P, bool transposed) const
	A generic implementation of jacobianAndPartials() for the case where all natural coordinates are independent, such as in line segments, quads and hexahedrons. More...

virtual void	jacDependentNatCoord (const GmVector &ncoord, const GmMatrix &X, GmMatrix &J, GmMatrix &P, bool transposed) const
	A generic implementation of jacobianAndPartials() for the case where all natural coordinates are NOT independent, such as in triangles and tetrahedrons. More...

bool	ginv (const GmMatrix &A, GmMatrix &inv) const
	Calculates the Moore-Penrose generalized matrix inverse for the 'm x n' matrix A, filling inv. More...

virtual bool	gradientBasedCartesianToNatural (const GmVector &coord, const GmMatrix &X, double tol, int maxIter, double natTol, GmVector &ncoord, bool *inside) const =0

bool	gradientBasedCartesianToNaturalQuadHex (const GmVector &coord, const GmMatrix &X, double tol, int maxIter, double natTol, GmVector &ncoord, bool *inside) const
	Given a set of cartesian coordinates 'coord' and a matrix with node coordinates 'X', calculates the corresponding natural coordinate filling 'ncoord'. Returns true if the calculation succeeded, false otherwise. More...

bool	gradientBasedCartesianToNaturalTriTet (const GmVector &coord, const GmMatrix &X, double tol, int maxIter, double natTol, GmVector &ncoord, bool *inside) const
	An implementation of the gradient based cartesian to natural algorithm specific to Tri and Tet elements. For a description of the algorithm and function parameters, see gradientBasedCartesianToNaturalQuadHex().

bool	gradientBasedCartesianToNaturalBar (const GmVector &coord, const GmMatrix &X, double tol, int maxIter, double natTol, GmVector &ncoord, bool *inside) const
	An implementation of the gradient based cartesian to natural algorithm specific to Bar elements. For a description of the algorithm and function parameters, see gradientBasedCartesianToNaturalQuadHex().

bool	gradientBasedCartesianToNaturalWedge (const GmVector &coord, const GmMatrix &X, double tol, int maxIter, double natTol, GmVector &ncoord, bool *inside) const
	An implementation of the gradient based cartesian to natural algorithm specific to Wedge elements. For a description of the algorithm and function parameters, see gradientBasedCartesianToNaturalQuadHex().

virtual bool	hasGeometryBasedCartesianToNatural () const
	A virtual function that should be replaced to return true if the shape implements a geometry based algorithm for converting cartesian coordinates to natural coordinates. In that case, geometryBasedCartesianToNatural() must also be reimplemented.

virtual bool	geometryBasedCartesianToNatural (const GmVector &coord, const GmMatrix &X, double natTol, GmVector &ncoord, bool *inside) const
	Virtual function that should be implemented if a shape can provide a geometric algorithm for converting cartesian coordinates to natural coordinates. See the cartesianToNatural() description for the arguments description.

bool	checkAndClampNaturalCoordinate (double &ncoord, double min, double max, double natTol) const
	An utilitary function that given a natural coordinate component and its domain (given by min and max), checks that coord is inside the interval, possibly clamping it to the domain if outside by a little bit, controled by the given tolerance. More...

bool	checkAndClampBarycentricNaturalCoordinates (GmVector &ncoord, double natTol) const
	An utilitary function that given a set of 3 or 4 barycentric natural coordinates, checks for out of the triangle/tetrahedron values, possibly clamping it to the domain if outside by a little bit, controled by the given tolerance. More...

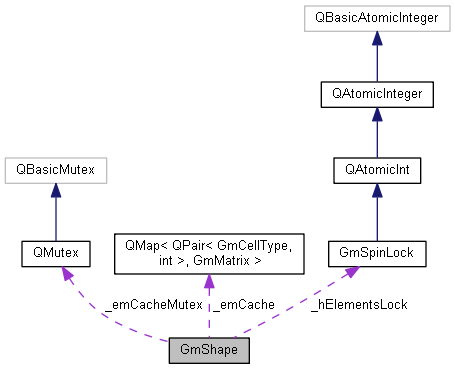
Static Private Attributes
static const void *	_shapePointersList [GM_NUM_CELL_TYPES]
	The global list with per element type shape pointers.

static GmSpinLock	_hElementsLock
	The spin-lock protecting the access/creation of shape pointers for hierarchical elements.

static bool	_preferGeometricConfig = false
	Should calls to cartesianToNatural prefer geometric algorithms (if available) over the gradient based one ?

static double	_gradTolConfig = 1e-6
	The convergence tolerance used by gradient based calls to cartesianToNatural.

static int	_maxGradIterConfig = 15
	The maximum number of iterations used by gradient based calls to cartesianToNatural.

static double	_outsideNatTolConfig = 0.0
	The "snap" tolerance used by cartesianToNatural to consider a point outside the element.

static QMap< QPair< GmCellType, int >, GmMatrix >	_emCache
	A global cache, keyed by cell type + cacheKey(), storing extrapolation matrices.

static QMutex	_emCacheMutex
	The mutex protecting _emCache.

Detailed Description

Shape function handling base classe.

When inheriting from this class, please make sure to also adjust the function GmShape::shapeFromElementType()

Member Function Documentation

◆ borderScalingFactor()

virtual double GmShape::borderScalingFactor	(	int	border,
		const GmVector &	borderCoord,
		const GmVector &	elementCoord,
		const GmMatrix &	X,
		bool	transposed = `false`
	)		const

pure virtual

Returns the scaling factor needed when calculating integrals over borders (edges or faces). This has the same effect as the jacobian determinant when integrating over the whole element. It can be used to treat 2D and 3D edge / face boundary conditions in a single code.

For 2D elements it is equivalent to edgeScalingFactor() and for 3D elements to faceScalingFactor(). This function is undefined for line elements.

Parameters

border	Defines the edge or face where the integration is taking place.
borderCoord	Defines the integration point where the factor will be calculated in the border (edge or face) reference system.
elementCoord	Defines the integration point where the factor will be calculated in the element reference system. It should have a dimension equal to numNaturalCoord().
X	The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix wher d is the number of dimension and n the number of shape functions. See the description given in jacobian().
transposed	If true, the X matrix should be the transposed of the matrix defined above.

Returns: Returns the calculated scaling factor

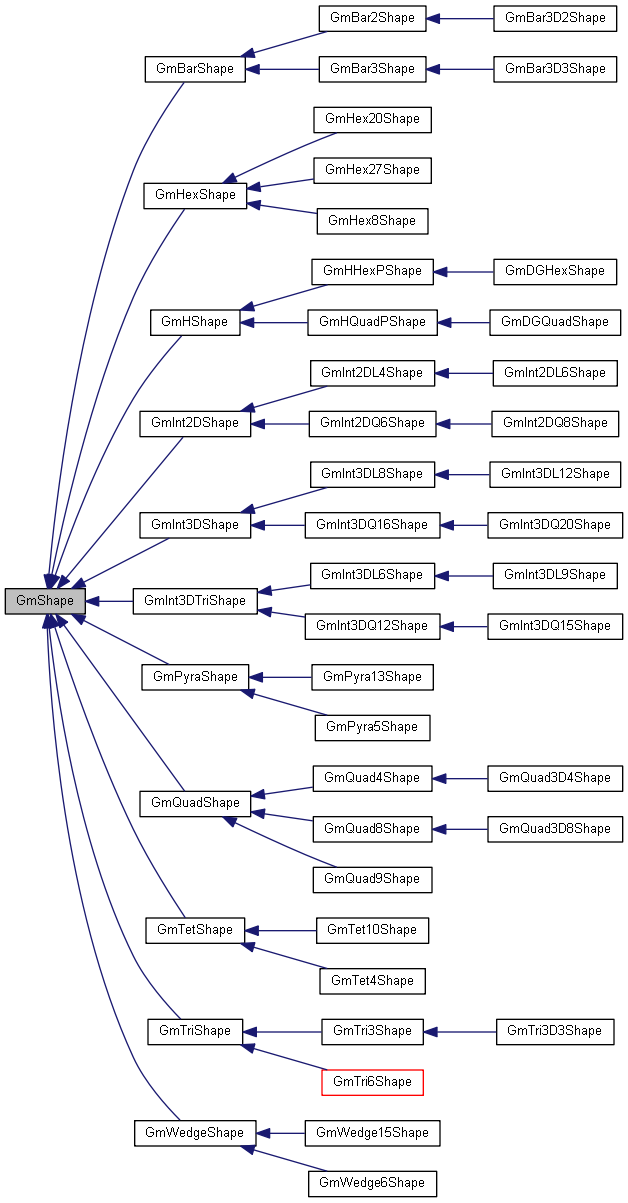
Implemented in GmHHexPShape, GmInt3DShape, GmInt3DTriShape, GmInt2DShape, GmBarShape, GmQuadShape, GmTriShape, GmWedgeShape, GmHQuadPShape, GmHexShape, GmTetShape, and GmPyraShape.

◆ cartesianToNatural() [1/2]

virtual bool GmShape::cartesianToNatural	(	const GmVector &	coord,
		const GmMatrix &	X,
		GmVector &	ncoord,
		bool *	inside
	)		const

inlinevirtual

Given a set of cartesian coordinates 'coord' and a matrix with node coordinates 'X', calculates the corresponding natural coordinate filling 'ncoord'. The inside parameter is filled with true if the given cartesian coordinate is inside the element, false otherwise.

This function uses either a geometric or a gradient based approach, depending on global configuration options read from the model when the shape module is initialized. For a finer control of the used algorithm, the overloaded version of this function can be used.

The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix where d is the number of cartesian coordinates and n the number of nodes. For a quad example it should be:

X = [x1, x2, x3, x4]

[y1, y2, y3, y4]

If ncoord holds a vector created by DECLARE_REF_VECTOR(), its size MUST already be equal to the expected result size (numNaturalCoord()).

This function should not be called before a call to GmShape::setConfigOptions(), but that should never be a problem since this is automatically done by the model loader just after model loading AND the shape functions are not available in the Lua environment during model loading.

The function returns false if there was an error calculating the natural coordinate (no convergence, for example).

◆ cartesianToNatural() [2/2]

virtual bool GmShape::cartesianToNatural	(	const GmVector &	coord,
		const GmMatrix &	X,
		bool	preferGeometric,
		double	gradTol,
		int	maxGradIter,
		double	outsideNatTol,
		GmVector &	ncoord,
		bool *	inside
	)		const

inlinevirtual

Given a set of cartesian coordinates 'coord' and a matrix with node coordinates 'X', calculates the corresponding natural coordinate filling 'ncoord'. The inside parameter is filled with true if the given cartesian coordinate is inside the element, false otherwise.

This function uses either a geometric or a gradient based approach, depending on the preferGeometric parameter. If preferGeometric is true AND a geometric algorithm is available, as defined by hasGeometryBasedCartesianToNatural(), the geometric version is used. Otherwise, a generic gradient based algorithm is used.

The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix where d is the number of cartesian coordinates and n the number of nodes. For a quad example it should be:

X = [x1, x2, x3, x4]

[y1, y2, y3, y4]

If ncoord holds a vector created by DECLARE_REF_VECTOR(), its size MUST already be equal to the expected result size (numNaturalCoord()).

The gradTol and maxGradIter parameters are used by the gradient based method to determine the tolerance and the maximum number of iterations used when seaching for the natural coordinate.

The outsideNatTol parameter, when greater than 0.0, gives a "snap" tolerance within which cartesian coordinates slightly outside the element will be snapped to the element border when converting cartesian to natural coordinates. For example, if the tolerance is 1e-3 and the conversion yields a natural coordinate of 1.0002, the coordinate will be changed to 1.0 and the point considered internal to the element. Keep in mind that this tolerance might not work for every type of element, especially with geometric methods and elements using barycentric coordinates.

The function returns false if there was an error calculating the natural coordinate (no convergence,for example).

◆ checkAndClampBarycentricNaturalCoordinates()

bool GmShape::checkAndClampBarycentricNaturalCoordinates	(	GmVector &	ncoord,
		double	natTol
	)		const

protected

An utilitary function that given a set of 3 or 4 barycentric natural coordinates, checks for out of the triangle/tetrahedron values, possibly clamping it to the domain if outside by a little bit, controled by the given tolerance.

If ncoord is inside the domain, returns true. If ncoord contains negative coordinates, but limited by -natTol, clamps the value to the triangle / tetrahedron and returns true Otherwise, returns false (keeping coord unchanged).

If natTol is zero, still uses the standard tolerance given by GmDoubleCmp::lte and gte

◆ checkAndClampNaturalCoordinate()

bool GmShape::checkAndClampNaturalCoordinate	(	double &	ncoord,
		double	min,
		double	max,
		double	natTol
	)		const

protected

An utilitary function that given a natural coordinate component and its domain (given by min and max), checks that coord is inside the interval, possibly clamping it to the domain if outside by a little bit, controled by the given tolerance.

If ncoord is inside the domain given by [min, max], returns true. If ncoord is inside the domain given by [min-natTol, max+natTol], clamps the value to [min, max] and returns true Otherwise, returns false (keeping coord unchanged).

If natTol is zero, still uses the standard tolerance given by GmDoubleCmp::lte and gte

◆ edgeScalingFactor()

virtual double GmShape::edgeScalingFactor	(	int	border,
		const GmVector &	borderCoord,
		const GmVector &	elementCoord,
		const GmMatrix &	X,
		bool	transposed = `false`
	)		const

pure virtual

Returns the scaling factor needed when calculating integrals over element edges. This has the same effect as the jacobian determinant when integrating over the whole element.

This function is undefined for line elements.

Parameters

border	Defines the edge where the integration is taking place.
borderCoord	Defines the integration point where the factor will be calculated in the edge reference system.
elementCoord	Defines the integration point where the factor will be calculated in the element reference system. It should have a dimension equal to numNaturalCoord().
X	The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix wher d is the number of dimension and n the number of shape functions. See the description given in jacobian().
transposed	If true, the X matrix should be the transposed of the matrix defined above.

Returns: Returns the calculated scaling factor

Implemented in GmTri6Shape, GmHHexPShape, GmTri3Shape, GmInt3DShape, GmInt3DTriShape, GmInt2DShape, GmBarShape, GmQuadShape, GmWedgeShape, GmHQuadPShape, GmHexShape, GmTetShape, and GmPyraShape.

◆ faceScalingFactor()

virtual double GmShape::faceScalingFactor	(	int	border,
		const GmVector &	borderCoord,
		const GmVector &	elementCoord,
		const GmMatrix &	X,
		bool	transposed = `false`
	)		const

pure virtual

Returns the scaling factor needed when calculating integrals over element faces. This has the same effect as the jacobian determinant when integrating over the whole element.

This function is undefined for line or 2D elements.

Parameters

border	Defines the face where the integration is taking place.
borderCoord	Defines the integration point where the factor will be calculated in the face reference system.
elementCoord	Defines the integration point where the factor will be calculated in the element reference system. It should have a dimension equal to numNaturalCoord().
X	The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix wher d is the number of dimension and n the number of shape functions. See the description given in jacobian().
transposed	If true, the X matrix should be the transposed of the matrix defined above.

Returns: Returns the calculated scaling factor

Implemented in GmHHexPShape, GmInt3DShape, GmInt2DShape, GmInt3DTriShape, GmBarShape, GmQuadShape, GmHQuadPShape, GmWedgeShape, GmTriShape, GmHexShape, GmTetShape, and GmPyraShape.

◆ fillNaturalCoordinates()

void GmShape::fillNaturalCoordinates	(	GmMatrix &	coord,
		bool	transposed = `false`
	)		const

Fills the coord matrix with the set of natural coordinates for the shape nodes.

The resulting matrix will have size equal to n x m where n is the number of shape functions (numFunctions()) and m is the number of natural coordinates (numNaturalCoord()). If coord holds a matrix created by DECLARE_REF_MATRIX(), its size MUST already be equal to the expected result size.

If transposed is set to true, the result will be a m x n matrix instead.

◆ gaussExtrapolationMatrix()

const GmMatrix & GmShape::gaussExtrapolationMatrix ( const GmIntegrationRule * ir ) const

virtual

Given an integration rule, compatible with the current element type, constructs an extrapolation matrix to calculate node values from integration point values.

This function works independently if the number of integration points is equal, greater or even smaller than the number of element nodes. See the description on pointExtrapolationMatrix() for an in-depth discussion of how the extrapolation matrix is built.

This function keeps a global cache of extrapolation matrices keyed by the element type and by the integration rule name. In this way, calling this function multiple times for an integration rule will return the same extrapolation matrix reference, and this reference is guaranteed to be valid the whole program lifetime.

If the extrapolation matrix could not be calculated, returns an empty matrix.

◆ ginv()

bool GmShape::ginv	(	const GmMatrix &	A,
		GmMatrix &	inv
	)		const

protected

Calculates the Moore-Penrose generalized matrix inverse for the 'm x n' matrix A, filling inv.

If m == n, ginv(A) = inv(A) If m > n, ginv(A) = inv(At . A) . At If m < n, ginv(A) = At . inv(A . At)

Either way, the resulting matrix will have size equal to 'n x m'. If inv holds a matrix created by DECLARE_REF_MATRIX(), its size MUST already be equal to the expected result size. Otherwise it will be resized to the correct size.

See equations 1 and 2 in "A local extrapolation method for finite elements", Durand & Farias, at Advances in Engineering Software, jan 2014.

If the inverse could not be calculated, returns false.

◆ gradientBasedCartesianToNaturalQuadHex()

bool GmShape::gradientBasedCartesianToNaturalQuadHex	(	const GmVector &	coord,
		const GmMatrix &	X,
		double	tol,
		int	maxIter,
		double	natTol,
		GmVector &	ncoord,
		bool *	inside
	)		const

protected

Given a set of cartesian coordinates 'coord' and a matrix with node coordinates 'X', calculates the corresponding natural coordinate filling 'ncoord'. Returns true if the calculation succeeded, false otherwise.

The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix where d is the number of cartesian coordinates and n the number of nodes. For a quad example it should be:

X = [x1, x2, x3, x4]

[y1, y2, y3, y4]

The tol, maxIter and natTol are tolerance values as described below. The inside parameter returns true if the coordinate is inside the element or false if outside.

If ncoord holds a vector created by DECLARE_REF_VECTOR(), its size MUST already be equal to the expected result size (numNaturalCoord()).

This implementation uses the element Jacobian transformation to iteratively calculate the natural coordinate. A more efficient, geometry aware, method can be used whenever possible.

Reference: "Efficient Inverse Isoparametric Mapping Algorithm for Whole-Body Computed Tomography Registration Using Deformations Predicted by Nonlinear Finite Element Modeling" Mao Li, Adam Wittek and Karol Miller - Journal of Biomechanical Engineering, august 2014

Method: Iterate over the equation n_k+1 = n_k + J_inv_k * (x - x_k) until |x - x_k| < tol, where:

n_k+1 are the natural coordinates at iteration k+1 n_k are the natural coordinates at iteration k J_inv_k is the inverse of the Jacobian matrix calculated at xi_k x are the cartesian coordinates of the searched point (coord) x_k are the cartesian coordinates of n_k

n_0 initial guess is given by the element centroid. We could try linearly interpolating x between the minimum and maximum element coordinate values and adjusting that between the natural coordinate limits (for elements whose natural coordinates are all not Barycentric), but that gets tricky when the natural axis are rotated with respect to the cartesian axis and so it seems not to be worthy.

The tol parameter controls the precision of the iteration. If more than maxIters are executed, the iteration loop is broken and the function returns false. The natTol parameter provides a "snap" tolerance to bring to the inside of the element values on the border that are slightly out of the element. Say, for example that the calculated natural coordinate first component is -1.0000001. If natTol is 1e-5, that componente will be snapped to the -1.0 border.

This implementation is specific to Quad and Hex elements. For alternative variations fpor other element types, see the other functions from this "family".

◆ initShapeFunctions()

bool GmShape::initShapeFunctions ( )

static

Initializes the shape function module. Must be called BEFORE any calls to shapeFromElementType() or linearShapeFromElementType(), but AFTER the static initialization of the geometry objects.

To obey the order in which this function must be called, we can't rely on a global static variable calling initShapeFunctions() (since we can't know if the geometry singleton objects where already created or not). Our solution is to explicitly call this function in the GmSimulation constructor.

◆ interpolate()

double GmShape::interpolate	(	const GmVector &	nodeValues,
		const GmVector &	ncoord
	)		const

Given a set of node values and a set of natural coordinates, interpolates the node values on the given coordinate.

Parameters

nodeValues	Vector filled with nodal values for the property beeing interpolated. Should have size equal to the number of nodes (also equal to numFunctions()) and ordered according to the node numbering schema defined on the shape documentation
ncoord	Vector filled with the natural coordinates over which the shape functions will be evaluated. Should have numNaturalCoord() entries

Returns: Returns the interpolated values

◆ jacDependentNatCoord()

void GmShape::jacDependentNatCoord	(	const GmVector &	ncoord,
		const GmMatrix &	X,
		GmMatrix &	J,
		GmMatrix &	P,
		bool	transposed
	)		const

protectedvirtual

A generic implementation of jacobianAndPartials() for the case where all natural coordinates are NOT independent, such as in triangles and tetrahedrons.

See Felippa, AFEM, Appendix I, table I.3 for more details.

Reimplemented in GmTri3D6Shape, and GmTri3D3Shape.

◆ jacIndependentNatCoord()

void GmShape::jacIndependentNatCoord	(	const GmVector &	ncoord,
		const GmMatrix &	X,
		GmMatrix &	J,
		GmMatrix &	P,
		bool	transposed
	)		const

protectedvirtual

A generic implementation of jacobianAndPartials() for the case where all natural coordinates are independent, such as in line segments, quads and hexahedrons.

See Felippa, AFEM, Appendix I, table I.3 for more details.

Reimplemented in GmQuad3D8Shape, and GmQuad3D4Shape.

◆ jacobian()

virtual void GmShape::jacobian	(	const GmVector &	ncoord,
		const GmMatrix &	X,
		GmMatrix &	J,
		bool	transposed = `false`
	)		const

inlinevirtual

Calculates the jacobian matrix, relating cartesian coordinates to natural coordinates.

The returned matrix is a square matrix with size equal to the number of natural coordinates, organised as can be seen bellow, for a Quad example with cartesian coordinates x, y and natural coordinates Xi, Eta (assumming a summation convention over the index i):

J = [ dx/dXi, dx/dEta ] = [ x_i * dN_i/dXi, x_i * dN_i/dEta]

[ dy/dXi, dy/dEta ] [ y_i * dN_i/dXi, y_i * dN_i/dEta]

See Felippa, AFEM, Appendix I, table I.3 for more details.

Partial derivatives are computed at the position specified by ncoord.

The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix where d is the number of cartesian coordinates and n the number of nodes. For the quad example it should be:

X = [x1, x2, x3, x4]

[y1, y2, y3, y4]

Such a matrix can be obtained by a call to GmCell::fillNodeMatrix(nodeAccessor, X, true).

If transposed == true, the X matrix should be the transpose of the matrix defined above and also the result will be the transpose of the J matrix above.

◆ jacobianAndPartials()

virtual void GmShape::jacobianAndPartials	(	const GmVector &	ncoord,
		const GmMatrix &	X,
		GmMatrix &	J,
		GmMatrix &	P,
		bool	transposed = `false`
	)		const

pure virtual

This function does the same calculations as the jacobian() call, but also filling the extra parameter P with the matrix of shape function partials.

When the user needs the partials P as well as the Jacobian matrix for its computations, this function saves the need to compute P twice (since it is used in the Jacobian computation).

The result matrix P has the same layout as a call to shapePartials(ncoord, P, transposed)

Implemented in GmInt3DShape, GmInt2DShape, GmInt3DTriShape, GmBarShape, GmQuadShape, GmHShape, GmTriShape, GmWedgeShape, GmHexShape, GmTetShape, and GmPyraShape.

◆ naturalCenter()

virtual void GmShape::naturalCenter ( GmVector & coord ) const

pure virtual

Fills the coord vector with the set of natural coordinates for the element center.

The resulting vector will have size equal to numNaturalCoord(). If coord holds a vector created by DECLARE_REF_VECTOR(), its size MUST already be equal to the expected result size.

Implemented in GmHHexPShape, GmHQuadPShape, GmWedgeShape, GmInt3DShape, GmInt3DTriShape, GmHexShape, GmInt2DShape, GmQuadShape, GmTetShape, GmTriShape, GmPyraShape, and GmBarShape.

◆ naturalToCartesian()

void GmShape::naturalToCartesian	(	const GmVector &	ncoord,
		const GmMatrix &	X,
		GmVector &	coord
	)		const

virtual

Given a set of natural coordinates 'ncoord' and a matrix with node coordinates 'X', calculates the corresponding cartesian coordinates filling 'coord'.

The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix where d is the number of cartesian coordinates and n the number of nodes. For a quad example it should be:

X = [x1, x2, x3, x4]

[y1, y2, y3, y4]

Calling this function is equivalent to calling interpolate() for each cartesian dimension. If coord holds a vector created by DECLARE_REF_VECTOR(), its size MUST already be equal to the expected number of cartesian dimensions.

The result vector coord might be the same vector as the input vector ncoord.

Reimplemented in GmInt3DShape, GmInt2DShape, GmInt3DTriShape, and GmHShape.

◆ nodeNaturalCoord()

virtual void GmShape::nodeNaturalCoord	(	int	node,
		GmVector &	coord
	)		const

pure virtual

Fills the coord vector with the set of natural coordinates for the reference shape function node. Node should be a value between 0 and numFunctions(). This is generally equal to the number of nodes but can be different for interface elements.

The resulting vector will have size equal to numNaturalCoord(). If coord holds a vector created by DECLARE_REF_VECTOR(), its size MUST already be equal to the expected result size.

Implemented in GmInt3DQ16Shape, GmInt2DQ6Shape, GmQuad9Shape, GmInt3DQ12Shape, GmBar3Shape, GmHex27Shape, GmQuad8Shape, GmTri6Shape, GmInt3DL8Shape, GmTet10Shape, GmInt2DL4Shape, GmWedge15Shape, GmInt3DL6Shape, GmPyra13Shape, GmHex20Shape, GmBar2Shape, GmQuad4Shape, GmHHexPShape, GmTri3Shape, GmWedge6Shape, GmHex8Shape, GmTet4Shape, GmPyra5Shape, and GmHQuadPShape.

◆ pointExtrapolationMatrix()

bool GmShape::pointExtrapolationMatrix	(	const GmMatrix &	points,
		GmMatrix &	em
	)		const

virtual

Given the set of 'm' natural coordinates in points, builds an 'n x m' extrapolation matrix that can be used to extrapolate values from an 'm' sized value vector to the 'n' elements nodes.

Given a set of known values 'w', with size 'm x 1', calculated at the given points, returns a matrix M, with size 'n x m' that can be multipled by 'w' so that the result v = M.w contains a vector with size 'n x 1' with the calculated values at the 'n' element nodes.

The points matrix should be a matrix with size 'd x m' where 'd' is the number of shape function natural coordinates and 'm' is the number of known values. The result matrix 'em' will have size equal to 'n x m' where 'n' is the number of element nodes. If em holds a matrix created by DECLARE_REF_MATRIX(), its size MUST already be equal to the expected result size. Otherwise it will be resized to the correct size.

Conceptually, the problem modeled by this function is to find the solution for the following equation system: w = N.v, where w (m x 1) is the vector of known values, N (m x n) is the shape function matrix with each row storing the shape function values calculated at each w point coordinate, and v (n x 1) is the desired vector with nodal values.

If the number of points is equal to the number of nodes, the returned matrix will be simply equal to inv(N). If m > n, the equation system is overdetermined and the result is obtained by least squares method, minimizing the reconstruction error for w results when recovered by node value interpolation. If m < n, the number of equations is smaller than the number of unknowns and the adopted solution follows the method proposed at the paper by Durand & Farias.

See equations 13 (m > n) and 36 (m < n) in "A local extrapolation method for finite elements", Durand & Farias, at Advances in Engineering Software, jan 2014.

Returns false if the extrapolation matrix could not be calculated.

◆ scaledJacobianDet()

virtual double GmShape::scaledJacobianDet ( const GmMatrix & J ) const

pure virtual

Returns the Jacobian determinant multiplied by the scaling factor needed for transforming the differential area element. dOmega = dx.dy = J.dXi.dEta where J is the scaled Jacobian determinant.

See Felippa AFEM, appendix I, table I.3 / section I.2.4 or Felippa IFEM, chapters 17 (eq 17.20) and 24 (eq 24.7).

Implemented in GmInt2DShape, GmBarShape, GmInt3DShape, GmHShape, GmQuadShape, GmTriShape, GmWedgeShape, GmInt3DTriShape, GmHexShape, GmTetShape, and GmPyraShape.

◆ shapeCartesianPartialsFromCoord()

double GmShape::shapeCartesianPartialsFromCoord	(	const GmVector &	ncoord,
		const GmMatrix &	X,
		GmMatrix &	dN,
		bool	transposed = `false`
	)		const

virtual

Function used to calculate shape function partial derivatives with respect to its cartesian coordinates, evaluated at the given point.

Results are placed in the dN matrix. It's size will be equal to n x d, where 'n' is the number of nodes of this element and 'd' is the number of cartesian coordinates. In that way, line 'i' holds the set of partial derivatives of the shape function Ni with respect to all of its cartesian coordinates.

As an example, for a quad 4 element, this function evaluates the shape function cartesian derivatives with respect to x and y, evaluated at the point (xi, eta). The result matrix will have size equal to 4 x 2 and values equal to:

[dN1/dx, dN1/dy]
[dN2/dx, dN2/dy]
[dN3/dx, dN3/dy]
[dN4/dx, dN4/dy]

The X matrix gives the cartesian coordinates of every node and should be organized as a 'd x n' matrix where d is the number of cartesian coordinates and n the number of nodes. For the quad example it should be:

X = [x1, x2, x3, x4]

[y1, y2, y3, y4]

If transposed == true, the result matrix will be created transposed. Also, the supplied X matrix should be the transposed of the format above.

IMPORTANT: In general this function doesn't need to be reimplemented in derived classes since its implementation is based on shapeCartesianPartialsFromPJ(), which MUST be reimplemented by every shape type.

Parameters

ncoord	Vector filled with the natural coordinates over which the shape function partials will be evaluated. Should have numNaturalCoord() entries.
X	The cartesian coordinates of the element nodes. See comments above for its format. Please rememeber that the expected format depends also on the transposed parameter.
dN	Matrix filled with partial derivatives. If dN holds a matrix created by DECLARE_REF_MATRIX(), its size MUST already be equal to the expected size.
transposed	If true, the result matrix will be transposed (and the X matrix format also).

Returns: Returns the scaled Jacobian determinant, often used together with the shape cartesian partials.

This is the same value returned by a call to scaledJacobianDet() but reusing the Jacobian matrix used while calculating the shape cartesian partials.

◆ shapeCartesianPartialsFromJacobian()

double GmShape::shapeCartesianPartialsFromJacobian	(	const GmVector &	ncoord,
		const GmMatrix &	J,
		GmMatrix &	dN,
		bool	transposed = `false`
	)		const

virtual

Alternative version of shapeCartesianPartials() to calculate shape function partial derivatives with respect to its cartesian coordinates, given a previously calculated Jacobian matrix.

This function is very usefull when working with super-parametric elements where the jacobian is calculated using the 'native' element shape functions but the field values are calculated with a linear shape function.

IMPORTANT: In general this function doesn't need to be reimplemented in derived classes since its implementation is based on shapeCartesianPartialsFromPJ(), which MUST be reimplemented by every shape type.

Parameters

ncoord	Vector filled with the natural coordinates over which the shape function partials will be evaluated. Should have numNaturalCoord() entries.
J	The Jacobian matrix, formated with the same transposed parameter passed to this function.
dN	Matrix filled with partial derivatives. If dN holds a matrix created by DECLARE_REF_MATRIX(), its size MUST already be equal to the expected size.
transposed	If true, the result matrix will be transposed (and the J matrix format also).

Returns: Returns the scaled Jacobian determinant, often used together with the shape cratesian partials. This is the same value returned by a call to scaledJacobianDet(J).

◆ shapeCartesianPartialsFromPJ()

virtual double GmShape::shapeCartesianPartialsFromPJ	(	const GmMatrix &	P,
		const GmMatrix &	J,
		GmMatrix &	dN,
		bool	transposed = `false`
	)		const

pure virtual

Alternative version of shapeCartesianPartialsXxxx() to calculate shape function partial derivatives with respect to its cartesian coordinates, given a previously calculated Jacobian matrix and a previously calculated shape function partial matrix.

This is the basic WORKER function for the previous two overloads. On a physics calculation calling one of the other two family functions is probably better...

Parameters

P	The shape functions natural partials matrix, formated with the same transposed parameter passed to this function.
J	The Jacobian matrix, formated with the same transposed parameter passed to this function.
dN	Matrix filled with partial derivatives. If dN holds a matrix created by DECLARE_REF_MATRIX(), its size MUST already be equal to the expected size.
transposed	If true, the result matrix will be transposed (and the J matrix format also).

Returns: Returns the scaled Jacobian determinant, often used together with the shape cratesian partials. This is the same value returned by a call to scaledJacobianDet(J).

Implemented in GmHHexPShape, GmHQuadPShape, GmInt2DShape, GmBarShape, GmInt3DShape, GmQuadShape, GmTriShape, GmWedgeShape, GmInt3DTriShape, GmHexShape, GmTetShape, and GmPyraShape.

◆ shapePartials()

virtual void GmShape::shapePartials	(	const GmVector &	ncoord,
		GmMatrix &	dN,
		bool	transposed = `false`
	)		const

pure virtual

Function used to calculate shape function partial derivatives with respect to its natural coordinates, evaluated at the given point.

Results are placed in the dN matrix. It's size will be equal to m x n, where 'm' is the number of functions (usually equal to the number of nodes of this element) and 'n' is the number of natural coordinates of this element.

In that way, line 'i' holds the set of partial derivatives of the shape function Ni with respect to all of its natural coordinates.

As an example, for a quad 4 element with Xi and Eta natural coordinates, this function evaluates the shape function partial derivatives with respect to Xi and Eta, evaluated at the point (xi, eta). The result matrix will have size equal to 4 x 2 and values equal to:

[dN1/dXi, dN1/dEta]
[dN2/dXi, dN2/dEta]
[dN3/dXi, dN3/dEta]
[dN4/dXi, dN4/dEta]

If transposed == true, the result matrix will be created transposed.

Parameters

ncoord	Vector filled with the natural coordinates over which the shape function partials will be evaluated. Should have numNaturalCoord() entries.
dN	Matrix filled with partial derivatives. If dN holds a matrix created by DECLARE_REF_MATRIX(), its size MUST already be equal to the expected size.
transposed	If true, the result matrix will be the transposed

Implemented in GmInt3DQ16Shape, GmInt2DQ6Shape, GmQuad9Shape, GmInt3DQ12Shape, GmBar3Shape, GmQuad8Shape, GmHex27Shape, GmTri6Shape, GmHHexPShape, GmInt3DL8Shape, GmTet10Shape, GmInt2DL4Shape, GmWedge15Shape, GmInt3DL6Shape, GmPyra13Shape, GmHex20Shape, GmBar2Shape, GmQuad4Shape, GmTri3Shape, GmWedge6Shape, GmHex8Shape, GmTet4Shape, GmPyra5Shape, and GmHQuadPShape.

◆ shapeValues()

virtual void GmShape::shapeValues	(	const GmVector &	ncoord,
		GmVector &	N
	)		const

pure virtual

Function used to evaluate the set of shape functions over a point defined by its natural coordinates.

Results are placed in the N vector. It's size will be equal to n, where n is the number of nodes of this element. If N holds a vector created by DECLARE_REF_VECTOR(), its size MUST already be equal to the expected result size.

Parameters

ncoord	Vector filled with the natural coordinates over which the shape functions will be evaluated. Should have numNaturalCoord() entries.
N	Vector with size equal to numFunctions() (which is usually equal to the number of nodes in the element, but can be different like in the interface elements case) that will be filled with the calculated shape functions

Implemented in GmInt3DQ16Shape, GmInt2DQ6Shape, GmQuad9Shape, GmInt3DQ12Shape, GmBar3Shape, GmQuad8Shape, GmHex27Shape, GmTri6Shape, GmInt3DL8Shape, GmHHexPShape, GmTet10Shape, GmInt2DL4Shape, GmWedge15Shape, GmInt3DL6Shape, GmPyra13Shape, GmHex20Shape, GmBar2Shape, GmQuad4Shape, GmTri3Shape, GmWedge6Shape, GmHex8Shape, GmTet4Shape, GmPyra5Shape, and GmHQuadPShape.

◆ translateEdgePoint()

virtual bool GmShape::translateEdgePoint	(	int	edge,
		const GmVector &	srcEdgeCoord,
		GmVector &	elementCoord
	)		const

pure virtual

Given a "bar like" edge coordinate (from -1 to 1), at the given edge, fills elementCoord with the equivalent element natural coordinate. Should be implemented for 2D & 3D elements.

Parameters

edge	The number of the edge for the source edge coordinate
srcEdgeCoord	The edge coordinate (single value, from -1 to 1).
elementCoord	The vector to be filled with element coordinates equivalent to srcEdgeCoord. After filled, elementCoord will be a vector with size equal to numNaturalCoord().

Returns: Returns true on success or false if the given edge SHOULD NOT be used for integration, like the "0 length" side edges for a closed 2d interface element.

Implemented in GmHHexPShape, GmHQuadPShape, GmWedgeShape, GmInt2DShape, GmInt3DShape, GmInt3DTriShape, GmHexShape, GmQuadShape, GmTetShape, GmTriShape, GmPyraShape, and GmBarShape.

◆ translateFacePoint()

virtual bool GmShape::translateFacePoint	(	int	face,
		const GmVector &	srcFaceCoord,
		GmVector &	elementCoord
	)		const

pure virtual

Given a "quad like" or "tri like" face coordinate (-1 to 1 pair for quad faces and 0 to 1 barycentric triple for tri faces), at the given face, fills elementCoord with the equivalent element natural coordinate. Should be implemented for 3D elements.

Parameters

face	The number of the face for the source face coordinate
srcFaceCoord	The face coordinate (-1 to 1 pair for quad faces and 0 to 1 barycentric triple for tri faces).
elementCoord	The vector to be filled with element coordinates equivalent to srcFaceCoord. After filled, elementCoord will be a vector with size equal to numNaturalCoord().

Returns: Returns true on success or false if the given face SHOULD NOT be used for integration, like the "0 area" side faces for a closed 3d interface element.

Implemented in GmHHexPShape, GmHQuadPShape, GmInt2DShape, GmWedgeShape, GmBarShape, GmInt3DShape, GmQuadShape, GmTriShape, GmInt3DTriShape, GmHexShape, GmTetShape, and GmPyraShape.

The documentation for this class was generated from the following files:

inc/elements/shape/gmShape.h
src/elements/shape/gmShape.cpp

Public Member Functions

Static Public Member Functions

Protected Member Functions

Static Private Attributes

Detailed Description

Member Function Documentation

◆ borderScalingFactor()

◆ cartesianToNatural() [1/2]

◆ cartesianToNatural() [2/2]

◆ checkAndClampBarycentricNaturalCoordinates()

◆ checkAndClampNaturalCoordinate()

◆ edgeScalingFactor()

◆ faceScalingFactor()

◆ fillNaturalCoordinates()

◆ gaussExtrapolationMatrix()

◆ ginv()

◆ gradientBasedCartesianToNaturalQuadHex()

◆ initShapeFunctions()

◆ interpolate()

◆ jacDependentNatCoord()

◆ jacIndependentNatCoord()

◆ jacobian()

◆ jacobianAndPartials()

◆ naturalCenter()

◆ naturalToCartesian()

◆ nodeNaturalCoord()

◆ pointExtrapolationMatrix()

◆ scaledJacobianDet()

◆ shapeCartesianPartialsFromCoord()

◆ shapeCartesianPartialsFromJacobian()

◆ shapeCartesianPartialsFromPJ()

◆ shapePartials()

◆ shapeValues()

◆ translateEdgePoint()

◆ translateFacePoint()